 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 1000 点
問題文
N 個の球と N+1 個の穴が一直線上に並んでいます。球には左から順に 1 から N の番号が、穴には左から順に 1 から N+1 の番号が振られています。i 番の球は i 番の穴と i+1 番の穴の間に置かれており、隣り合う穴と球の間の距離を左から順に並べて得られる数列を d_i (1 \leq i \leq 2 \times N) とおきます。d_1 の値とパラメータ x が与えられており、d_i - d_{i-1} = x が任意の i (2 \leq i \leq 2 \times N) に対して成り立っています。
これら N 個の球を 1 個ずつ転がし、穴に落としていくことを考えます。球が穴の上を通ると、その穴にすでに別の球が入っていなければその穴に落ちます。すでに別の球がその穴に入っていた場合は、球は落ちずにそのまま転がり続けます。(なお、この問題で考える球の転がし方において、球どうしが衝突することはありません。)
球を転がす際は、まだ転がされていない球の中から等確率で 1 つを選び、その球を左または右に等確率で転がします。これを N 回繰り返してすべての球を転がすとき、すべての球が移動する距離の総和の期待値を求めてください。
以下に N = 3, d_1 = 1, x = 1 の場合の球の転がし方の例を挙げます。
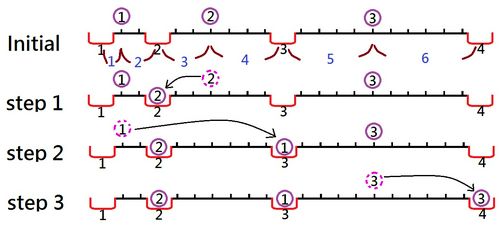
- 2 番の球を左に転がす。球は 2 番の穴に落ちる。球が移動する距離は 3 である。
- 1 番の球を右に転がす。球は 2 番の穴の上を通り、3 番の穴に落ちる。球が移動する距離は 9 である。
- 3 番の球を右に転がす。球は 4 番の穴に落ちる。球が移動する距離は 6 である。
この例では、球が移動する距離の総和は 18 となります。
なお、球をどのように転がしてもどの球も必ずいずれかの穴に落ち、最後に穴が一つだけ空のまま残ることになります。
制約
- 1 \leq N \leq 200,000
- 1 \leq d_1 \leq 100
- 0 \leq x \leq 100
- 入力値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N d_1 x
出力
答えを小数で出力せよ。絶対誤差または相対誤差のいずれかが 10^{-9} 以内でなければならない。
入力例 1
1 3 3
出力例 1
4.500000000000000
球が 1 個、穴が 2 個あります。球から左の穴までの距離は 3 、球から右の穴までの距離は 6 です。球を左に転がすか右に転がすかの 2 通りの転がし方があり、それぞれにおいて球が移動する距離は 3, 6 です。したがって、答えは (3+6)/2 = 4.5 となります。
入力例 2
2 1 0
出力例 2
2.500000000000000
入力例 3
1000 100 100
出力例 3
649620280.957660079002380
Score : 1000 points
Problem Statement
There are N balls and N+1 holes in a line. Balls are numbered 1 through N from left to right. Holes are numbered 1 through N+1 from left to right. The i-th ball is located between the i-th hole and (i+1)-th hole. We denote the distance between neighboring items (one ball and one hole) from left to right as d_i (1 \leq i \leq 2 \times N). You are given two parameters d_1 and x. d_i - d_{i-1} is equal to x for all i (2 \leq i \leq 2 \times N).
We want to push all N balls into holes one by one. When a ball rolls over a hole, the ball will drop into the hole if there is no ball in the hole yet. Otherwise, the ball will pass this hole and continue to roll. (In any scenario considered in this problem, balls will never collide.)
In each step, we will choose one of the remaining balls uniformly at random and then choose a direction (either left or right) uniformly at random and push the ball in this direction. Please calculate the expected total distance rolled by all balls during this process.
For example, when N = 3, d_1 = 1, and x = 1, the following is one possible scenario:

- first step: push the ball numbered 2 to its left, it will drop into the hole numbered 2. The distance rolled is 3.
- second step: push the ball numbered 1 to its right, it will pass the hole numbered 2 and drop into the hole numbered 3. The distance rolled is 9.
- third step: push the ball numbered 3 to its right, it will drop into the hole numbered 4. The distance rolled is 6.
So the total distance in this scenario is 18.
Note that in all scenarios every ball will drop into some hole and there will be a hole containing no ball in the end.
Constraints
- 1 \leq N \leq 200,000
- 1 \leq d_1 \leq 100
- 0 \leq x \leq 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N d_1 x
Output
Print a floating number denoting the answer. The relative or absolute error of your answer should not be higher than 10^{-9}.
Sample Input 1
1 3 3
Sample Output 1
4.500000000000000
The distance between the only ball and the left hole is 3 and distance between the only ball and the right hole is 6. There are only two scenarios (i.e. push left and push right). The only ball will roll 3 and 6 unit distance, respectively. So the answer for this example is (3+6)/2 = 4.5.
Sample Input 2
2 1 0
Sample Output 2
2.500000000000000
Sample Input 3
1000 100 100
Sample Output 3
649620280.957660079002380